Monostatic Measurement of the Polarized Bidirectional Reflection Distribution Function
Monostatic Measurement of the Polarized Bidirectional Reflection Distribution Function by Oscar G. Rodríguez-Herrera and J. Scott Tyo
Controlling the spatial coherence and polarization of electromagnetic waves sheds new light on the measurement of the polarized bidirectional reflection distribution function in remote sensing.
The polarized bidirectional reflection distribution function (pBRDF) is widely used to characterize the scattering properties of materials and to model remote sensing engagements. Knowledge of a material’s pBRDF enables estimation of the signatures within a scene by adding information about the source-target-sensor geometry. The pBRDF (or its scalar cousin, the unpolarized BRDF) is generally used as a modeling tool, but it is also a powerful identifier that can be used to discriminate objects of interest in complicated scenes. In these situations, we could compare an experimentally measured scattering distribution with a pBRDF library, as is currently done for hyperspectral imaging. Unfortunately, remote measurement of the pBRDF is simply not possible in most real-world scenarios where the target is far away and not under the control of the sensing system.
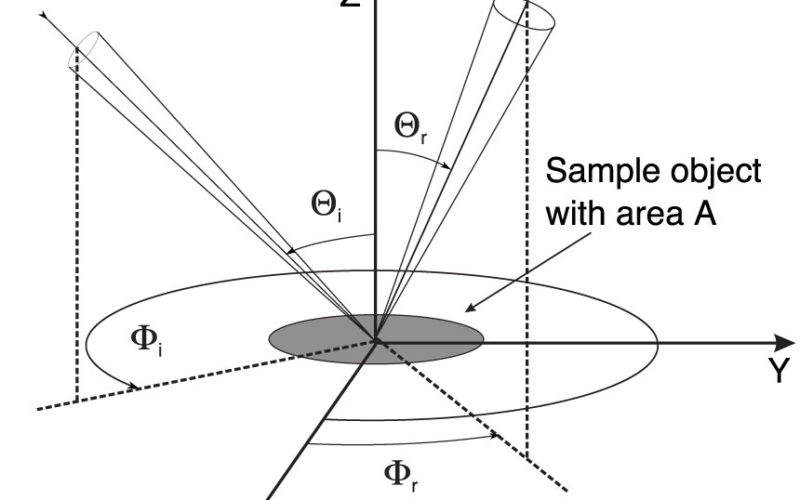
Typically, we measure the pBRDF of a target using goniometric (angle-measuring) setups, where we move the detection arm around the object to measure the light scattered at different angles for each angular position of the illumination arm. Figure 1 is a diagram of the goniometric configuration. We then use the measurements obtained at different angles of incidence to compute the pBRDF of the object. In remote sensing applications, the source of illumination and detector are enclosed in a single compact case (as in an artificial satellite, for example) that cannot be freely moved around a scene. Furthermore, in this case the illumination and detection arms are, by any practical means, parallel. Therefore, measurement of the pBRDF in real-life scenarios imposes more restrictions than its measurement in the laboratory, and ideally it should be obtained from monostatic measurements (using a radar system in which transmitter and receiver are collocated). To achieve this goal, we have introduced variable coherence polarimetry (VCPol), a technique that exploits the ability to control the spatial coherence and polarization properties of electromagnetic waves to achieve monostatic measurements of the pBRDF.
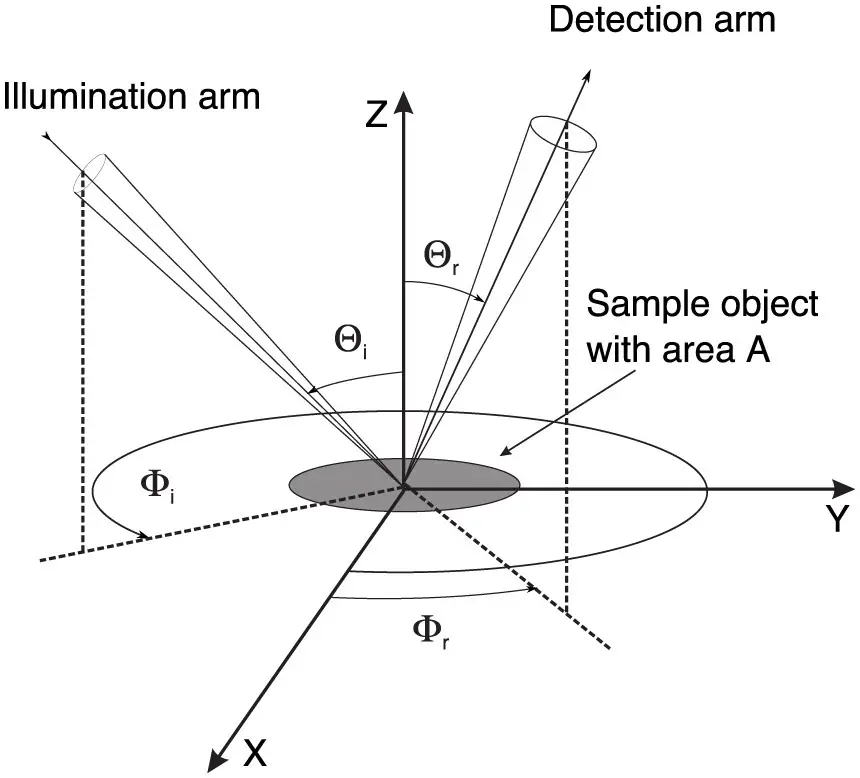
Figure 1. Diagram representing a typical configuration used to measure the polarized bidirectional reflection distribution function (pBRDF) of a sample object with area A. Θi, r, Φi, r are the polar and azimuth angles of the incident and reflected beams.
VCPol was introduced by Tyo and Turner as an extension of variable coherence tomography (VCT)—where the spatial coherence properties of the illumination are varied by adjusting the source’s intensity distribution—to include polarization of the illumination and the scattered field.1–3 VCPol manipulates the second-order statistical properties of the electromagnetic field to directly probe the second-order statistical properties of an object described by a scattering tensor F(r), which represents the target’s material properties. The innovation of VCPol is that the second-order statistical properties can be inferred from remote, single-point, monostatic measurements of the coherence matrix of the scattered field. The ability to control the coherence properties of the illumination enables development of a tomographic reconstruction whereby many different projections of F(r) are taken, from the same point of observation, by changing the coherence properties of the source.1
Fundamental to VCPol is the control of the spatial coherence and polarization properties of the illumination. In VCT, spatial coherence is controlled using the generalized van Cittert-Zernike theorem of optics, which was established for scalar sources but does not include information on the polarization of the field. We propose extending this theorem in terms of the cross-spectral density matrix to include polarization properties of quasi-homogeneous, planar electromagnetic sources.4 According to the extended theorem, the spatial coherence and polarization properties of the propagated field are related to the spectral density of the x- and y-polarization components of the source via Fourier transform. Therefore, it is possible to control the spatial coherence and polarization of the illumination in a VCPol experiment by changing the spectral density of the source.
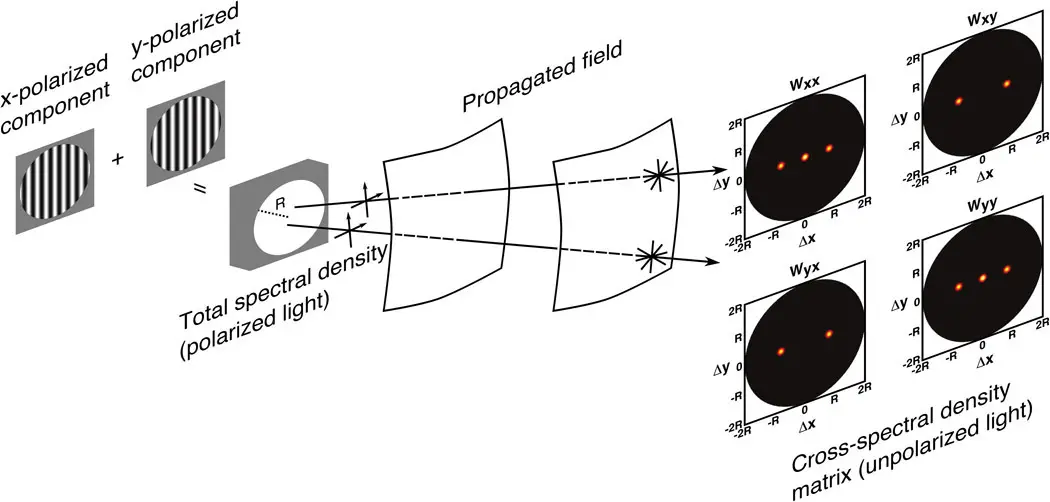
Figure 2. Diagram of a source designed using the generalized van Cittert-Zernike theorem for the cross-spectral density matrix and the resulting propagated field. Two sets of vertical x- and y-polarized fringes are added to create a quasi-homogeneous source with uniform total spectral density. The field produced by this source propagates, creating a field that is unpolarized in the usual single-point sense but polarized in the two-point sense away from the source. The propagated field is represented by the cross-spectral density matrix on the figure (with components Wxx, Wxy, Wyx, and Wyy). Due to the geometry of the spectral density fringes in this example, vector Δr0 is along the x-direction. The characteristics of this field are useful to perform the measurements required in variable coherence polarimetry for the monostatic determination of the pBRDF. R: Radius of of the circular aperture at source.
We have modeled quasi-homogeneous sources that produce electromagnetic fields with second-order statistical properties suitable for application in VCPol.4 For example, we have modeled a source that creates a field that is unpolarized in the usual single-point sense but polarized in the two-point sense.5 That is, a field for which the x- and y-components at a single point within the beam are uncorrelated, whereas the x- and y-components at a point P1 are independently correlated with the x- and y-components at another point P2, within the beam, separated from P1 by a vector Δr0, which depends on the spectral density distribution of the source. We can create such fields with a source like the one depicted in Figure 2.4
Our current and future efforts include experimental validation of the ability to control the spatial coherence and polarization properties of the illumination, the simulation of engagement scenarios in remote sensing, the development of data processing methods, verification of the VCPol technique, and the design of a system capable of performing VCPol outside the laboratory.
This work was supported by the Air Force Office of Scientific Research under grant FA9550-10-0114.
University of Arizona
Oscar G. Rodríguez-Herrera is a postdoctoral research associate at the College of Optical Sciences. He received a BS and an MS in physics from the Universidad Nacional Autónoma de México and a PhD in experimental physics from the National University of Ireland, Galway.
J. Scott Tyo is a professor at the College of Optical Sciences. He holds a BSE, an MSE, and a PhD in electrical engineering from the University of Pennsylvania.
