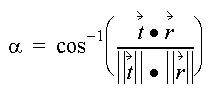Introduction
Hyperspectral remote sensing is the science of acquiring digital imagery of earth materials in many narrow contiguous spectral bands. Hyperspectral sensors or imaging spectrometers measure earth materials and produce complete spectral signatures with no wavelength omissions. Such instruments are flown aboard space and air-based platforms. Handheld versions also exist and are used for accuracy assessment missions and small scale investigations.
Hyperspectral remote sensing instruments are typical with several contiguous bands in all parts of the spectrum in which they operate. Digital Airborne Imaging Spectrometer, for example, is hyperspectral, having 63 bands, 27 in the visible, and near infra-red (0.4-1.0 microns), two in the short wave infrared (1.0-1.6 microns), 28 in the short wave infrared important for mapping clay minerals (2.0-2.5 microns), and 6 in the thermal infrared. The ability to measure reflectance in several contiguous bands across a specific part of the spectrum allows these instruments to produce a spectral curve that can be compared to reference spectra for any number of minerals, thereby allowing the mineral content of a particular piece of ground to be determined.
Hyperspectral remote sensing involves breaking a broadband from the visible and infra-red into hundreds of spectral parts, which allows a very precise match of ground characteristics, such as color, to the reference standards. The technique is so sensitive that it can detect camouflaged objects and has been used in forestry to measure biomass and damage caused by plant disease. Hyperspectral remote sensing combines imaging and spectroscopy in a single system, which often includes large data sets and require new processing methods. Hyperspectral data sets are generally composed of about 100 to 200 spectral bands of relatively narrow bandwidths (5-10 nm), whereas, multispectral data sets are usually composed of about 5 to 10 bands of relatively large bandwidths.
General Spectroscopy
The field of spectroscopy is divided into emission and absorption spectroscopy. An emission spectrum is obtained by spectroscopic analysis of some light source. This phenomenon is primarily caused by the excitation of atoms by thermal or electrical means; absorbed energy causes electrons in a ground state to be promoted to a state of higher energy level. The lifetime of electrons in this metastable state is short, and they return to some lower state or to the ground state; the absorbed energy is released as light. An absorption spectrum is obtained by placing the substance between the sensor and some source of energy that provides EMR in the frequency range being studied. The sensor analyzes the transmitted energy relative to the incident energy for a given frequency.
So for studying the various spectral curves, we have to take care of absorption spectrum of various features, the peak absorption can be because of :
1. Charge transfer absorptions
2. Electron transition absorptions and
3. Vibrational absorptions.
Spectroscopy is the study of electromagnetic radiation. Spectrometry is derived from spectro-photometry, the measure of photons as a function of wavelength, a term used for years in astronomy. However, spectrometry is becoming a term used to indicate the measurement of non-light quantities, such as in mass spectrometry. Terms like laboratory spectrometer, spectroscopist, reflectance spectroscopy, thermal emission spectroscopy, etc, are in common use. Researchers are studying and applying methods for identifying and mapping materials through spectroscopic remote sensing (called imaging spectroscopy, hyperspectral imaging, imaging spectrometry, etc), on the earth and throughout the solar system using laboratory, airborne and spacecraft spectrometers.
The solar spectrum from 400 to 2500 nm provides enough surface irradiance to permit spectral imaging in reflected sunlight, and the hyperspectral sensor covering this spectrum will have on the order of 200 spectral bands. It aims to improve the accuracy and the extend the scope of terrestrial remote sensing by fully exploiting the spectral domain, while providing the spectral information in the spatial context so that it can be readily interpreted and used.
There are 4 general parameters that describe the capability of a spectrometer:
1) Spectral range,
2) Spectral bandwidth,
3) Spectral sampling, and
4) Signal-to-noise ratio (S/N).
Spectral range is important to cover enough diagnostic spectral absorption to solve a desired problem. There are general spectral ranges that are in common use, each to first order controlled by detector technology: a) ultraviolet (UV): 0.001 to 0.4 µm, b) visible: 0.4 to 0.7 µm, c) near-infrared (NIR): 0.7 to 3.0 µm, d) the mid-infrared (MIR): 3.0 to 30 µm, and d) the far infrared (FIR): 30 µm to 1 mm (e.g. see The Photonics Design and Applications Handbook, 1996 and The Handbook of Chemistry and Physics, any recent year). The ~0.4 to 1.0-µm wavelength range is sometimes referred to in the remote sensing literature as the VNIR (visible-near-infrared) and the 1.0 to 2.5-µm range is sometimes referred to as the SWIR (short-wave infrared). It should be noted that these terms are not recognized standard terms in other fields except remote sensing, and because the NIR in VNIR conflicts with the accepted NIR range, the VNIR and SWIR terms probably should be avoided. The mid-infrared covers thermally emitted energy, which for the Earth starts at about 2.5 to 3 µm, peaking near 10 µm, decreasing beyond the peak, with a shape controlled by grey-body emission.
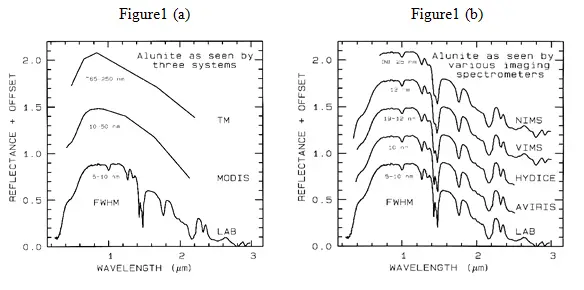
Spectral bandwidth is the width of an individual spectral channel in the spectrometer. The narrower the spectral bandwidth, the narrower the absorption feature the spectrometer will accurately measure, if enough adjacent spectral samples are obtained. Some systems have a few broad channels, not contiguously spaced and, thus, are not considered spectrometers (Figure 1a). Examples include the Landsat Thematic Mapper (TM) system and the MODerate Resolution Imaging Spectroradiometer (MODIS), which can’t resolve narrow absorption features. Others, like the NASA JPL Airborne Visual and Infra-Red Imaging Spectrometer (AVIRIS) system have many narrow bandwidths, contiguously spaced (Figure 1b). Figure 1 shows spectra for the mineral alunite that could be obtained by some example broadband and spectrometer systems. Note the loss in subtle spectral detail in the lower resolution systems compared to the laboratory spectrum. Bandwidths and sampling greater than 25 nm rapidly lose the ability to resolve important mineral absorption features. All the spectra in Figure 1b are sampled at half Nyquist (critical sampling) except the Near Infrared Mapping Spectrometer (NIMS), which is at Nyquist sampling. Note, however, that the fine details of the absorption features are lost at the ~25 nm bandpass of NIMS. For example, the shoulder in the 2.2-µm absorption band is lost at 25-nm bandpass. The Visual and Infrared Mapping Spectrometer (VIMS) and NIMS systems measure out to 5 µm, thus can see absorption bands not obtainable by the other systems.
List of Hyperspectral Sensors:
- HSI
- ARIES
- HYPERION
- CHRIS
- HYDICE
As new sensor technology has emerged over the past few years, high dimensional multispectral data with hundreds of bands have become available. For example, the AVIRIS system gathers image data in 210 spectral bands in the 0.4-2.4 µm range. Compared to the previous data of lower dimensionality (less than 20 bands), this hyperspectral data potentially provides a wealth of information. However, it also raises the need for more specific attention to the data analysis procedure if this potential is to be fully realized.
|
Table 1. Some hyperspectral systems deployed (12/00). |
|||
|
Sensor |
Wavelength range (nm) |
Band width (nm) |
Number of bands |
| AVIRIS | 400-2500 | 10 | 224 |
| TRWIS III | 367-2328 | 5.9 | 335 |
| HYDICE | 400-2400 | 10 | 210 |
| CASI | 400-900 | 1.8 | 288 |
| OKSI AVS | 400-1000 | 10 | 61 |
| MERIS | 412-900 | 10,7.5,15,20 | 15 |
| Hyperion | 325-2500 | 10 | 242 |
Hyperspectral Data
The data produced by imaging spectrometers is different from that of multispectral instruments owing to the enormous number of wavebands recorded. For a given geographical area imaged the data produced can be viewed as a cube, having two dimensions that represent spatial position and one that represents wavelength. Although data volume strictly does not pose any major data processing challenges with contemporary computing system it is nevertheless useful to examine the relative magnitudes of the data say TM and AVIRIS. Clearly, the major difference to note between the two is the number of wavebands (7 vs. 224) and the radiometric quantization (8 vs 10bpppb).Ignoring differences in spatial resolution, the relative data volumes, per pixel are 56:2240.Per pixel there are 40 times as many bits therefore for AVIRIS as for TM.
With 40 times as much data per pixel-does it means more information per pixel? Generally of course, that is not the case-much of the addional data does not add to the inherent information content for particular information even though it often helps in discovering that information in other words it contains redundancies. In remote sensing data redundancy can take two forms: spatial and spectral. Exploiting spatial redundancy is behind the spatial context methods. Spectral redundancy means that information content of one band can be fully or partly predicted from the other bands in the data.
Calibration
Calibrating imaging spectroscopy data to surface reflectance is an integral part of the data analysis process, and is vital if accurate results are to be obtained. The identification and mapping of materials and material properties is best accomplished by deriving the fundamental properties of the surface, its reflectance, while removing the interfering effects of atmospheric absorption and scattering, the solar spectrum, and instrumental biases. Calibration to surface reflectance is inherently simple in concept, yet it is very complex in practice because atmospheric radiative transfer models and the solar spectrum have not been characterized with sufficient accuracy to correct the data to the precision of some currently available instruments, such as the NASA/JPL Airborne Visible and Infra-Red Imaging Spectrometer.
The objectives of calibrating remote sensing data are to remove the effects of the atmosphere (scattering and absorption) and to convert from radiance values received at the sensor to reflectance values of the land surface. The advantages offered by calibrated surface reflectance spectra compared to uncorrected radiance data include: 1) the shapes of the calibrated spectra are principally influenced by the chemical and physical properties of surface materials, 2) the calibrated remotely-sensed spectra can be compared with field and laboratory spectra of known materials, and 3) the calibrated data may be analyzed using spectroscopic methods that isolate absorption features and relate them to chemical bonds and physical properties of materials. Thus, greater confidence may be placed in the maps of derived from calibrated reflectance data, in which errors may be viewed to arise from problems in interpretation rather than incorrect input data.
Data normalization:
When detailed radiometric correction is not feasible normalization is an alternative which makes the corrected data independent of multiplicative noise, such as topographic and solar spectrum effects. This can be performed using Log Residuals, based on the relationship between radiance and reflectance.
The number of training samples required to train a classifier for high dimensional data is much greater than that required for conventional data, and gathering these training samples can be difficult and expensive. Therefore, the assumption that enough training samples are available to accurately estimate the class quantitative description is frequently not satisfied for high dimensional data. The pre-labeled samples used to estimate class parameters and design a classifier are called training samples. The accuracy of parameter estimation depends substantially on the ratio of the number of training samples to the dimensionality of the feature space. As the dimensionality increases, the number of training samples needed to characterize the classes increase as well. If the number of training samples available fails to catch up with the need, which is the case for hyperspectral data, parameter estimation becomes inaccurate. Consider the case of a finite and fixed number of training samples. The accuracy of statistics estimation decreases as dimensionality increases, leading to a decline of the classification accuracy. Although increasing the number of spectral bands (dimensionality) As a result, the classification accuracy first grows and then declines as the number of spectral bands increases, which is often referred to as the Hughes phenomenon).
Spectral Libraries
The interpretation of high spectral resolution “hyperspectral” image data can be simplified by using examples from laboratory and ground acquired libraries of documented spectra referred to as spectral library.
Spectral libraries contain spectra of individual species that have been acquired at test sites representatives of varied terrain and climatic zones, observed in the field under natural conditions. Included also are other data description for example, construction materials, minerals vegetation and fabrics as observed in the laboratories under standardized conditions. Such library or database in combination with an software tool can enable in identification of materials by matching their spectra with remotely sensed data for identification purpose.
Analysis and Interpretation of Imaging Spectrometer Data
Different techniques have been designed to map the absorption features to make positive discrimination of surface reflectance targets. They are
Linear Spectral Unmixing Algorithm
The most widely used method for extracting surface information from remotely sensed images is image classification. The spectral characteristics of each training class are defined through statistical or probabilistic process from feature spaces and unknown pixel to be classified are statistically compared with known classes and assigned to the class to which they mostly resemble.
Natural surfaces are rarely composed of a single uniform material. Spectral mixing is a consequence of the mixing of materials having different spectral properties within the GIFOV [Ground instantaneous field of view] of a single pixel. If the scale of mixing is large [macroscopic], mixing occurs in linear fashion. For microscopic or intimate features mixing occurs in a non-linear fashion. Linear mixing refers to additive combinations of several diverse materials that occur in patterns too fine to be resolved by the sensors. The linear model assumes no interaction between materials. If each photon sees one material, these signals add [a linear process]. Multiple scattering involving several materials can be thought of as cascaded multiplications [a non-linear process].
What Causes Spectral Mixing
A variety of factors interact to produce the signal received by the imaging spectrometer
- A very thin volume of material interacts with incident sun light. All the materials present in this volume contribute to total reflected energy.
- Spatial mixing of materials in the area represented by a single pixel results in spectrally mixed reflected signals.
- Variable illumination due to topography [shade] and actual shadow in the area represented by the pixel further modify the reflected signal, basically mixing with a “black” end member.
- The imaging spectrometer integrates the reflected light from each pixel.
Spectral unmixing analysis is devoted to extracting pure spectra that by necessity form each image. It can be achieved only if the pixels are formed by linear mixing
Modelling Mixed Spectra
The simplest model of a mixed spectrum is a linear one, in which the spectrum is a linear combination of the “pure” spectra of the materials located in the pixel area, weighted by their fractional abundance. Mixture modelling aims at finding the mixed reflectance from a set of pure end-member-spectra.
A spectral library forms the initial data matrix for the analysis. The ideal spectral library contains end members that when linearly combined can form all other spectra. The mathematical model is a simple one. The observed spectrum [a vector] is considered to be the product of multiplying the mixing library of pure end member spectra [a matrix] by the end member abundance [a vector]. An inverse of the original spectral library matrix is formed by multiplying together the transposes of the orthogonal matrices and the reciprocal values of the diagonal matrix. A simple vector-matrix multiplication between the inverse library matrix and an observed mixed spectrum gives an estimate of the abundance of the library end members for the unknown spectrum.
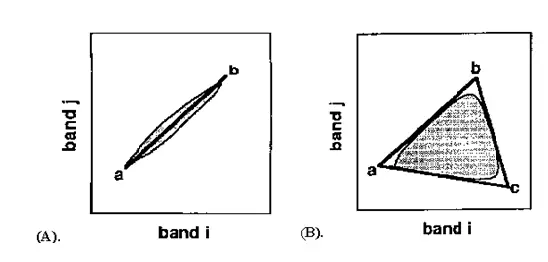
The geometric mixing model provides an alternate intuitive means to understand spectral mixing. Mixed pixels are visualized as points in n-dimensional scatter-plot space [spectral space], where n is the number of bands. In two dimensions, if only two end members mix, then the mixed pixels will fall in a line(fig 2A). The pure end members will fall at the two ends of the mixing line. If three end members mix, then the mixed pixels will fall inside a triangle(fig 2B). Mixtures of end members “fill in” between the end members.
Figure 2: End member selection using PCA
All mixed spectra are “interior” to the pure end members, inside the simplex formed by the end member vertices, because all the abundances are positive and sum to unity. This “convex set” of mixed pixels can be used to determine how many end members are present and to estimate their spectra. The geometric model is extensible to higher dimensions where the number of mixing end members is one more than the inherent dimensionally of the mixed data.
Spectral unmixing
Two very different types of unmixing are typically used: Using “known” end members and using “derived” end members.
Using known end members, one seeks to derive the apparent fractional abundance of each endmembers material in each pixel, given a set of “known” or assumed spectral endmembers. These known endmembers can be drawn from the data [averages of region picked using previous knowledge], drawn from a library of pure materials by interactively browsing through the imaging spectrometer data to determine what pure materials exist in the image, or determined using expert systems.
The mixing endmembers matrix is made up of spectra from the image or a reference library. The mixing matrix is inverted and multiplied by the observed spectra to get least-squares estimates of the unknown endmembers abundance fractions. Constraints can be placed on the solutions to give positive fractions that sum to unity. Shade and shadow are included either implicitly [fractions sum to 1 or less] or explicitly as an endmember [fraction sum to 1].
The second unmixing method uses the imaging spectrometer data themselves to “derive” the mixing endmembers . The inherent dimensionality of the data is determined using a special orthozonalization procedure related to principal components:
- A linear sub-space, or “flat” that spans the entire signal in the data is derived.
- The data are projected onto this subspace, lowering the dimensionality of the unmixing and removing most of the noise.
- The convex hull of these projected data is found.
- The data are “shrink-wrapped” by a simplex of n-dimensions, giving estimates of the pure endmembers.
- These derived endmembers must give feasible abundance estimates [positive fractions that sum to unity].
Spectral unmixing is one of the most promising hyperspectral analysis research areas. Analysis procedures using the convex geometry approach already developed for AVIRIS data have produced quantitative mapping results for a variety of materials [geology, vegetation, oceanography] with a priori knowledge. Combination of the unmixing approach with model-based data calibration and expert system identification capabilities could potentially result in an end-to-end quantitative yet automated analysis methodology.
Spectral Angle Mapper Classification
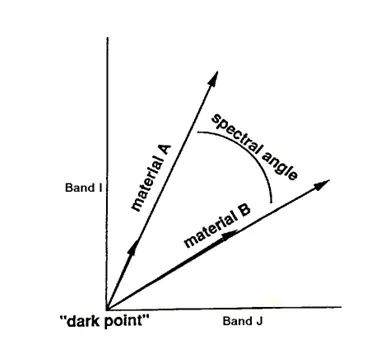
The Spectral Angle Mapper [SAM] is an automated method for comparing image spectra to individual spectra or a spectral library. Spectral angle mapping calculates the spectral similarity between a test reflectance spectrum and a reference reflectance spectrum. SAM assumes that the data have been reduced to apparent reflectance [true reflectance multiplied by some unknown gain factor controlled by topography and shadows]. The algorithm determines the similarity between two spectra by calculating the “spectral angle” between them, treating them as vectors in a space with dimensionality equal to the number of bands [nb]. A simplified explanation of this can be given by considering a reference spectrum and an unknown spectrum from two-band data. The two different materials will be represented in the 2-D scatter plot by a point for each given illumination, or as a line [vector] for all possible illuminations [Figure3].
Figure 3: 2-D Scatter plot
Because it uses only the “direction” of the spectra, and not their “length”, the method is insensitive to the unknown gain factor, and all possible illuminations are treated equally. Poorly illuminated pixels will fall closer to the origin. The “color” of a material is defined by the direction of its unit vector. The angle between the vectors is the same regardless of the length. The length of the vector relates only to how fully the pixel is illuminated.
The spectral similarity between an unknown spectrum t to a reference spectrum r, is expressed in terms of average angle µ between the two spectra
which also can be written as
Where nb equals the number of bands in the image.
For each reference spectrum chosen in the analysis of a hyperspectral image, the spectral angle a is determined for every image spectrum [pixel]. This value, in radians which gives a quantitative estimate of the presence of absorption features, is assigned to the corresponding pixel in the output SAM image, one output image for each reference spectrum. The derived spectral angle maps form a new data cube with the number of bands equal to the number of reference spectra used in the mapping. Grey-level thresholding is typically used to empirically determine those areas that most closely match the reference spectrum while retaining spatial coherence.
Application of Hyperspectral Image Analysis
1. Mineral targeting and mapping.
2. It can detect soil properties including moisture, organic content, and salinity.
3. Vegetation scientists have successfully used hyperspectral imagery to identify Vegetation species (Clark et al., 1995), study plant canopy chemistry (Aber and Martin, 1995), and
detect vegetation stress (Merton, 1999).
4. Military personnel have used hyperspectral imagery to detect military vehicles under partial vegetation canopy, and many other military target detection objectives.
5. Atmosphere: Study of atmospheric parameters such as clouds, aerosol conditions and Water vapour for monitoring long term, large-scale atmospheric variations as a result of
environmental change. Study of cloud characteristics, i.e. structure and its distribution.
6. Ocenography: Measurement of photosynthetic potential by detection of phytoplankton, detection of yellow substance and detection of suspended matter. Investigations of water
quality, monitoring coastal erosion.
7. Snow and Ice: Spatial distribution of snow cover, surface albedo and snow water equivalent. Calculation of energy balance of a snow pack, estimation of snow properties-snow grain
size, snow depth and liquid water content.
8. Oil Spills: When oil spills in an area effected by wind, waves, and tides, a rapid and assessment of the damage can help to maximize the cleanup efforts. Environmentally
sensitive areas can be targeted for protection and cleanup, and the long-term damage can be minimized. Time sequence images of the oil can guide efforts in real-time by
providing relative concentrations and accurate location.
References
1.Rechards, John.R, and Jia, X., 1999:Remote Sensing Digital Image Analysis, Springer
2.Schowengerdt, Robert.A, 1997:Remote Sensing Modals and Methods for Image Processing, Academic Press.
3.Tong,Q.,Tian,Q.,Pu,O., and zhao,C.,2001,Spectrscopic determination of wheat Water status using 1650-1850 nm spectral absorption features, Int.J.Rs, Vol
22,No.12, 2329-2338
4.Dyer, Johen.R.,1994:Application of absorption Spectroscopy of Organic Compounds, Prentice Hall of India.
5.Curran, Paul.J.,2001,Imaging spectrometry for ecological application,JAG,Vol.3-Issue 4,305-312
6. http://speclab.cr.usgs.gov/spectral-lib.html for spectral library